py.CGAL.visual :: Pure Python KD-trees

EucleiDIs

EucleiDIs is a python geometric library which imitates CGAL. We are trying to have the ease of python coding with the capabilities of CGAL.

In the library section you can have a look of the classes,functions, exceptions of our library. For every class will be have all the functions properties and outputs

In the examples section you will have the opportunity to see or watch the library in action with as many examples we will be able to create

If you want to contact us do not hesitate to see in the contact us area.

The name is coming from the person whose name is strongly attached to geometry (Eucleides) and the name of our department (DI).

Show Hide

Library

Show/Hide

Classes

Point_2 Show/Hide

Definition

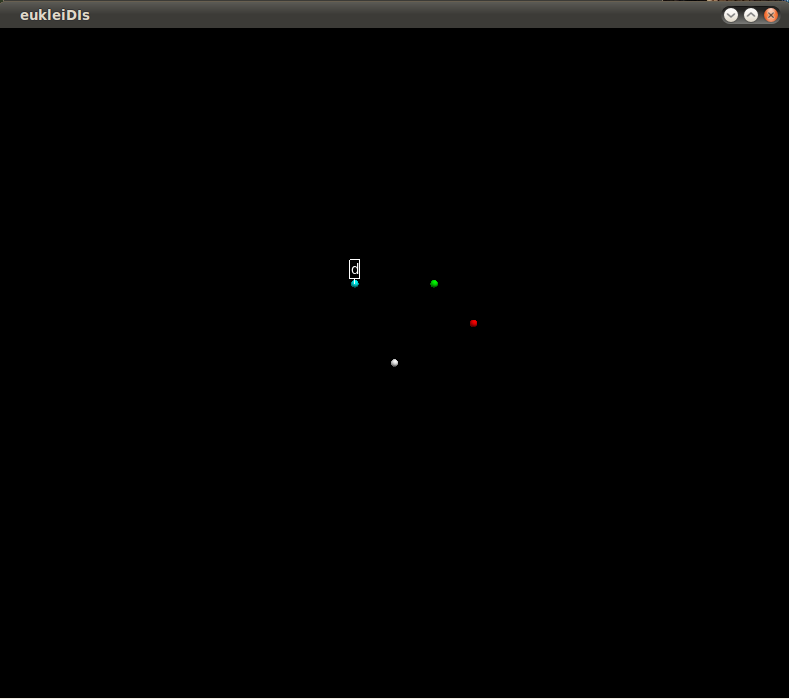
An object of the class Point_2 is a point in the two-dimensional Euclidean plane.

Constructor

p = Point_2(x=0,y=0,color=(1,1,1),visible=True) The contructor of the Point_2 object has as arguments the position of the point in the 2 dimensional space, the color of which the bullet will be colored and the visibility of the bullet.

Operators

bool p==q Returns true if p and q Point_2 objects has the same coordinates. Returns false otherwise.

bool p!=q Returns true if p and q Point_2 objects has not the same coordinates. Returns false otherwise.

bool p≤q Returns true if p coordinates are lesser or equal than q. Returns false otherwise.

bool p≥q Returns true if p coordinates are greater or equal than q. Returns false otherwise.

bool p<q Returns true if p coordinates are lesser than q. Returns false otherwise.

bool p>q Returns true if p coordinates are greater than q. Returns false otherwise.

Point_2 p+v p is Point_2 and v is Vector_2. Returning the point obtained by translating p by the vector v. Else raises exception.

Point_2 p-v p is Point_2 and v is Vector_2. Returning the point obtained by translating p by the vector -v. Else raises exception.

Vector_2 p-q p and q are Point_2. Returning the difference vector between p and q. Else raises exception.

float p[ int i ] Returns the i coordinate (0≤i≤1).

Operations

float p.x() Returns the x coordinate.

float p.y() Returns the y coordinate.

float p.cartesian( int i ) Returns the i coordinate (0≤i≤1).

int p.dimension() Returns 2.

sphere p.pos() Returns the visual python object sphere that Point_2 has as representation.

void p.visual(visible=None) If the argument ommitted then it reverses the visibility. Otherwise makes the visibility as the argument defines.

void p.label("label") Creates a label with the argument string for the Point_2 p.

void p.color(x=0,y=0,z=0) If color is called as p.color() prints the color of the Point_2
If it is called with with tuple (color.green) or (256,0,0) then it changes the color of the Point_2.
If you want to color a Point_2 black use the visualfunction(make it invisible).

Point_2 Library Top
Segment_2 Show/Hide

Definition

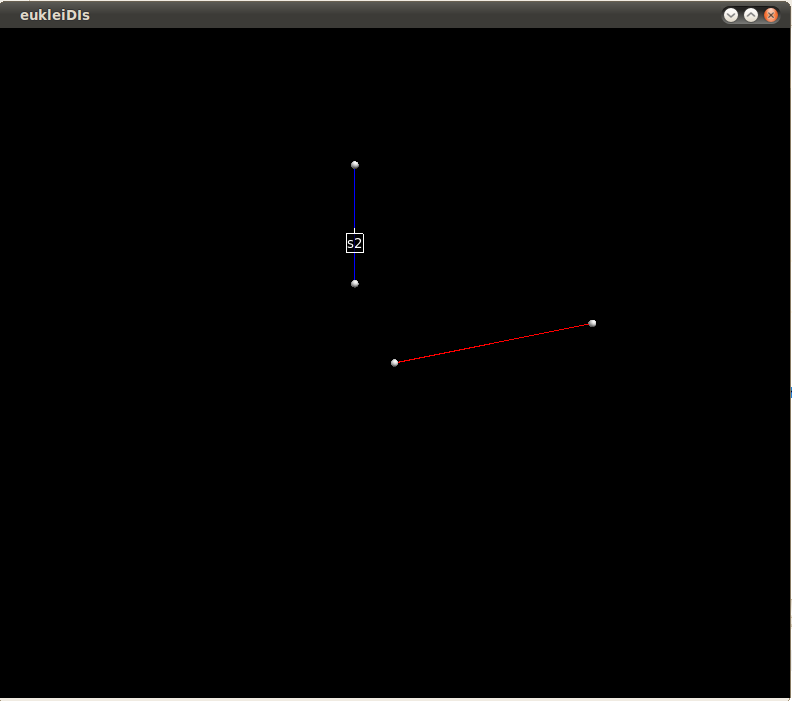
An object of the class Segment_2 is a directed straight line segment in the two-dimensional Euclidean plane 2, i.e. a straight line segment [p,q] connecting two points p,q in R 2. The segment is topologically closed, i.e. the end points belong to it. Point p is called the source and q is called the target of s. The length of s is the Euclidean distance between p and q. Note that there is only a function to compute the square of the length, because otherwise we had to perform a square root operation which is not defined for all number types, which is expensive, and may not be exact.

Constructor

s = Segment_2(<Point_2> source,<Point_2> target, color=(1,1,1), visible=True) The constructor of Segment_2 class has as arguments 2 Point_2 objects for the source and target points. Also has the color of the line will be colored and the visibility of the line.

Operations

Point_2 s.source() Returns the source of s.

Point_2 s.target() Returns the target of s.

Point_2 s.min() Returns the point of s with lexicographically smallest coordinate.

Point_2 s.max() Returns the point of s with lexicographically largest coordinate.

Point_2 s.middle() Returns the point which is in the middle of s.

Point_2 s.vertex( int i ) Returns source or target of s: vertex(0) returns the source of s, vertex(1) returns the target of s.

Point_2 s.point( int i ) Returns the vertex(i).

float s.squared_length() Returns the squared length of s.

Direction_2 s.direction() Returns the direction from source to target of s.

Vector_2 s.to_vector() Returns the vector s.target() - s.source().

Segment_2 s.opposite() Returns a segment with source and target point interchanged.

Line_2 s.supporting_line() Returns the line l passing through s. Line l has the same orientation as segment s.

void s.visual(visible=None) If the argument ommitted then it reverses the visibility. Otherwise makes the visibility as the argument defines.

void s.label("label") Creates a label with the argument string for the Segment_2 p.

void s.color(x=0,y=0,z=0) If color is called as p.color() prints the color of the Segment_2
If it is called with with tuple (color.green) or (256,0,0) then it changes the color of the Segment_2.
If you want to color a Segment_2 black use the visualfunction(make it invisible).

Predicates

bool s.is_degenarate() Segment s is degenerate, if source and target are equal.

bool s.is_horizontal()

bool s.is_vertical()

bool s.has_on(Point_2 p) A point is on s, iff it is equal to the source or target of s, or if it is in the interior of s.

Segment_2 Library Top
Vector_2 Show/Hide

Definition

An object of the class Vector_2 is a vector in the two-dimensional vector space. Geometrically spoken, a vector is the difference of two points p2, p1 and denotes the direction and the distance from p1 to p2.

Constructor

v = Vector_2(<Point_2> a, <Point_2> b, visible=True) Introduces the vector b-a.

v = Vector_2(int a, int b, visible=True)Introduces a vector v initialized to (x,y).

v = Vector_2(float a, float b, visible=True)Introduces a vector v initialized to (x,y).

v = Vector_2(<Segment_2> s, visible=True) Introduces the vector s.target()-s.source().

v = Vector_2(<Ray_2> r, visible=True)Introduces the vector having the same direction as r.

v = Vector_2(<Line_2> l, visible=True)Introduces the vector having the same direction as l.

Operators

bool v==w Returns true if v and w Vector_2 objects are the same object. Returns false otherwise.

Vector_2 v+w Addition of 2 vectors.

Vector_2 v-w Subtraction of 2 vectors.

int v*w V and w are both Vector_2 objects. It returns the inner product of the vectors.

Vector_2 v*<int> w Simple scalar multiplication of the vector is returned.

Vector_2 v/<int> w Simple scalar division of the vector is returned.

Vector_2 -v Returns the opposite vector.

float v[ int i ] Returns the i coordinate (0≤i≤1).

Operations

float v.x() Returns the x coordinate.

float v.y() Returns the y coordinate.

float v.cartesian( int i ) Returns the i coordinate (0≤i≤1).

int v.dimension() Returns 2.

Direction_2 v.direction() Returns the direction which passes through v.

float v.squared_length() Returns the squared length of v.

float v.angle() Returns the angle of v with the x axis in degrees.

Vector_2 Library Top
Direction_2 Show/Hide

Definition

An object of the class Direction_2 is a vector in the two-dimensional vector space where we forget about its length. They can be viewed as unit vectors, although there is no normalization internally, since this is error prone. Directions are used whenever the length of a vector does not matter. They also characterize a set of parallel oriented lines that have the same orientations. For example, you can ask for the direction orthogonal to an oriented plane, or the direction of an oriented line. Further, they can be used to indicate angles. The slope of a direction is dy()/dx().

Constructor

d = Direction_2(<Segment_2> s) Introduces the direction d of segment s.

d = Direction_2(<Vector_2> v) Introduces the direction d of vector v.

d = Direction_2(<Line_2> l) Introduces the direction d of line l.

d = Direction_2(<Ray_2> r) Introduces the direction d of ray r.

d = Direction_2(<int> x, <int> y) Introduces a direction d passing through the origin and the point with Cartesian coordinates (x, y).

Operators

bool d==e Returns true if d and e Direction_2 objects has the same coordinates. Returns false otherwise.

bool d!=e Returns true if p and e Direction_2 objects has not the same coordinates. Returns false otherwise.

bool d≤e Returns true if d coordinates are lesser or equal than e. Returns false otherwise.

bool d≥e Returns true if d coordinates are greater or equal than e. Returns false otherwise.

bool d<e Returns true if d coordinates are lesser than e. Returns false otherwise.

bool d>e Returns true if d coordinates are greater than e. Returns false otherwise.

Direction_2 -d Returns the opposite direction.

Operations

float d.delta(int i) Returns values, such that d== Direction_2(delta(0),delta(1)). (0≤i≤1)

float d.dx() Returns delta(0).

float d.dy() Returns delta(1).

bool d.counterclockwise_in_between ( d1, d2) Returns true, iff d is not equal to d1, and while rotating counterclockwise starting at d1, d is reached strictly before d2 is reached. Note that true is returned if d1 == d2, unless also d == d1.

Vector_2 d.to_vector() Returns a vector that has the same direction as d.

Direction_2 Library Top
Triangle_2 Show/Hide

Definition

An object t of the class Triangle_2 is a triangle in the two-dimensional Euclidean plane. Triangle t is oriented, i.e., its boundary has clockwise or counterclockwise orientation. We call the side to the left of the boundary the positive side and the side to the right of the boundary the negative side.

The boundary of a triangle splits the plane in two open regions, a bounded one and an unbounded one.

Constructor

t = Triangle_2(<Point_2> p,<Point_2> q, color=(1,1,1), visible=True) Introduces a triangle t with vertices p, q and r.

Operators

bool t1==t2 Test for equality: two triangles are equal, iff there exists a cyclic permutation of the vertices of t2, such that they are equal to the vertices of t.

bool t1!=t2 Test for inequality.

Point_2 t[int i] Returns vertex(i).

Operations

Point_2 t.vertex(int i) Returns the i'th vertex modulo 3 of t.

Triangle_2 t.opposite() Returns a triangle where the boundary is oriented the other way round (this flips the positive and the negative side, but not the bounded and unbounded side).

float t.area() Returns the signed area of t (with the help of Heron Formula).

void t.fill(x,y,z) If color is called as p.fill() prints the color of the Triangle_2
If it is called with with tuple (color.green) or (256,0,0) then it changes the filling of the Triangle_2.

void t.poi_color(x,y,z) If color is called as p.fill() prints the color of the points Triangle_2
If it is called with with tuple (color.green) or (256,0,0) then it changes the color of the points of the Triangle_2.

void t.seg_color(x,y,z) If color is called as p.fill() prints the color of the segments Triangle_2
If it is called with with tuple (color.green) or (256,0,0) then it changes the color of the segments of the Triangle_2.

Predicates

bool t.is_degenerate() Triangle t is degenerate, if the vertices are collinear.

Orientation t.orientation() Returns the orientation of t.

Oriented side t.oriented_side(<Point_2> p) Returns ON_ORIENTED_BOUNDARY, or POSITIVE_SIDE, or the constant ON_NEGATIVE_SIDE, determined by the position of point p. Precondition: t is not degenerate.

Bounted side t.bounded_side(<Point_2> p) Returns the constant ON_BOUNDARY, ON_BOUNDED_SIDE, or else ON_UNBOUNDED_SIDE, depending on where point p is. Precondition: t is not degenerate.

bool t.has_on_positive_side(<Point_2> p) bool t.has_on_negative_side(<Point_2> p) bool t.has_on_boundary(<Point_2> p) bool t.has_on_bounded_side(<Point_2> p) bool t.has_on_unbounded_side(<Point_2> p)

Triangle_2 Library Top
Line_2 Show/Hide

Definition

An object l of the data type Line_2 is a directed straight line in the two-dimensional Euclidean plane. It is defined by the set of points with Cartesian coordinates (x,y) that satisfy the equation l : ax + by + c = 0

The line splits two-dimensional Euclidean plane in a positive and a negative side. A point p with Cartesian coordinates (px, py) is on the positive side of l, iff a px + b py + c > 0, it is on the negative side of l, iff a px + b py + c < 0. The positive side is to the left of l.

Constructor

l = Line_2(int a, int b, int c color=(1,1,1), visible=True) Introduces a line l with the line equation in Cartesian coordinates ax +by +c = 0.

l = Line_2(<Point_2> p,<Point_2> q, color=(1,1,1), visible=True) Introduces a line l passing through the points p and q. Line l is directed from p to q

l = Line_2(<Point_2> p,<Direction_2> d,color=(1,1,1), visible=True) Introduces a line l passing through point p with direction d.

l = Line_2(<Point_2> p,<Vector_2> v, color=(1,1,1), visible=True) Introduces a line l passing through point p and oriented by v.

l = Line_2(<Segment_2> s, color=(1,1,1), visible=True) Introduces a line l supporting the segment s, oriented from source to target.

l = Line_2(<Ray_2> r, color=(1,1,1), visible=True) Introduces a line l supporting the ray r, with same orientation.

Operators

bool l==h Test for equality: Two lines are equal, iff the intersection of the lines are a line.

bool l!=h Test for inequality.

Operations

int l.a() Returns the first coefficient of l.

int l.b() Returns the second coefficient of l.

int l.c() Returns the third coefficient of l.

int l.x_at_y() Returns the x-coordinate of the point at l with given y-coordinate. Precondition: l is not horizontal.

int l.y_at_x() Returns the y-coordinate of the point at l with given x-coordinate. Precondition: l is not vertical.

Point_2 l.point(int i) Returns an arbitrary point on l. It holds point(i) == point(j), iff i==j. Furthermore, l is directed from point(i) to point(j), for all i < j.

Point_2 l.projection(<Point_2> p) Returns the orthogonal projection of p onto l.

Vector_2 l.to_vector() Returns a vector that has the direction of l.

Direction_2 l.direction() Returns the direction of l.

Line_2 l.opposite() Returns the line with opposite direction.

Line_2 l.perpendicular(<Point_2> p) Returns the line perpendicular to l and passing through p, where the direction is the direction of l rotated counterclockwise by 90 degrees.

Predicates

bool l.is_degenerate() Line l is degenerate, if the coefficients a and b of the line equation are zero.

bool l.is_horizontal()

bool l.is_vertical()

Oriented side l.oriented_side(<Point_2> p) Returns ON_ORIENTED_BOUNDARY, ON_NEGATIVE_SIDE, or the constant ON_POSITIVE_SIDE, depending on the position of p relative to the oriented line l.
For convenience we provide the following Boolean functions:
bool l.has_on(<Point_2> p)

bool l.has_on_positive_side(<Point_2> p)

bool l.has_on_negative_side(<Point_2> p)

Line_2 Library Top
Ray_2 Show/Hide

Definition

An object r of the data type Ray_2 is a directed straight ray in the two-dimensional Euclidean plane. It starts in a point called the source of r and goes to infinity.

Constructor

r = Ray_2(<Point_2> p,<Point_2> q, color=(1,1,1), visible=True) Introduces a ray r with source p and passing through point q.

r= Ray_2(<Point_2> p,<Direction_2> d,color=(1,1,1), visible=True) Introduces a ray r starting at source p with direction d.

r = Ray_2(<Point_2> p,<Vector_2> v, color=(1,1,1), visible=True) Introduces a ray r starting at source p with the direction of v.

r = Ray_2(<Point_2> p,<Line_2> l, color=(1,1,1), visible=True) Introduces a ray r starting at source p with the same direction as l.

Operators

bool r==h Test for equality: two rays are equal, iff they have the same source and the same direction.

bool r!=h Test for inequality.

Operations

Vector_2 r.to_vector() Returns a vector that has the direction of r.

Direction_2 r.direction() Returns the direction of r.

Ray_2 r.opposite() Returns the ray with the same source and the opposite direction.

Line_2 r.supporting_line() Returns the line supporting r which has the same direction.

Predicates

bool r.is_degenerate() Ray r is degenerate, if the source and the second defining point fall together (that is if the direction is degenerate).

bool r.is_horizontal()

bool r.is_vertical()

bool r.has_on(<Point_2> p) A point is on r, iff it is equal to the source of r, or if it is in the interior of r.

Ray_2 Library Top
Circle_2 Show/Hide

Definition

An object of type Circle_2 is a circle in the two-dimensional Euclidean plane. The circle is oriented, i.e. its boundary has clockwise or counterclockwise orientation . The boundary splits 2 into a positive and a negative side, where the positive side is to the left of the boundary. The boundary also splits 2 into a bounded and an unbounded side. Note that the circle can be degenerated, i.e. the squared radius may be zero.

Constructor

c = Circle_2(<Point_2> center,(int|float) squared_radius, Orientation ori = COUNTERCLOCKWISE, color=(1,1,1), visible=True) Introduces a variable c of type Circle_2. It is initialized to the circle with center center, squared radius squared_radius and orientation ori. Precondition: ori ≠ COLLINEAR, and further, squared_radius greater or equal 0.

c = Circle_2(<Point_2> p,<Point_2> q,Orientation ori = COUNTERCLOCKWISE, color=(1,1,1), visible=True) Introduces a variable c of type Circle_2. It is initialized to the circle with diameter pq and orientation ori. Precondition: ori ≠ COLLINEAR.

c = Circle_2(<Point_2> p, <Point_2> q ,<Point_2> r, color=(1,1,1), visible=True) Introduces a variable c of type Circle_2. It is initialized to the unique circle which passes through the points p, q and r. The orientation of the circle is the orientation of the point triple p, q, r. Precondition: p, q, and r are not collinear.

c = Circle_2(<Point_2> center, Orientation ori, color=(1,1,1), visible=True) Introduces a variable c of type Circle_2. It is initialized to the circle with center center, squared radius zero and orientation ori. Precondition: ori ≠ COLLINEAR. Postcondition: c.is_degenerate() = true.

Operators

bool c==circle2 Returns true, iff c and circle2 are equal, i.e. if they have the same center, same squared radius and same orientation .

bool c!=circle2 Returns true, iff c and circle2 are not equal.

Operations

Point_2 c.center() Returns the center of c.

int | float c.squared_radius() Returns the squared radius of c.

Orientation c.orientation() Returns the orientation of c.

Circle_2 c.opposite() Returns the circle with the same center and squared radius as c but with opposite orientation.

Predicates

bool c.is_degenerate() Returns true, iff c is degenerate, i.e. if c has squared radius zero.

Oriented side c.oriented_side(<Point_2> p) Returns either the constant ON_ORIENTED_BOUNDARY, ON_POSITIVE_SIDE, or ON_NEGATIVE_SIDE, iff p lies on the boundary, properly on the positive side, or properly on the negative side of c, resp.

Bounted side c.bounded_side(<Point_2> p) Returns ON_BOUNDED_SIDE, ON_BOUNDARY, or ON_UNBOUNDED_SIDE iff p lies properly inside, on the boundary, or properly outside of c, resp.

bool c.has_on_positive_side(<Point_2> p) bool c.has_on_negative_side(<Point_2> p) bool c.has_on_boundary(<Point_2> p) bool c.has_on_bounded_side(<Point_2> p) bool c.has_on_unbounded_side(<Point_2> p)

Circle_2 Library Top
Polygon_2 Show/Hide

Definition

An object pgn of the data type Polygon_2 is a plane figure that is bounded by a closed path or circuit, composed of a finite sequence of straight line segments.

Constructor

pgn = Polygon_2(<Point_2 list> points,<Segment_2 list> segments=None, color=(1,1,1), visible=True) Introduces a polygon pgn with vertices from the list points. The segments list can be filled with the output of getPolygon function.

Operators

bool p1==p2 Test for equality: two polygons are equal iff there exists a cyclic permutation of the vertices of p2 such that they are equal to the vertices of p1. Note that the template argument Container of p1 and p2 may be different.

bool p1!=p2 Test for inequality.

Point_2 p[ int i] Returns the i-th vertex.

Operations

float pgn.area() Returns the signed area of the polygon pgn. This means that the area is positive for counter clockwise polygons and negative for clockwise polygons.

int pgn.size() Returns the number of vertices of the polygon pgn.

Point_2 p[ int i] Returns the i-th vertex.

Point_2 p.vertex(int i) Returns the i-th vertex.

Segment_2 p.edge(int i) Returns the i-th edge.

Polygon_2 p.reverse_orientation() Reverses the orientation of the polygon. The vertex pointed to by p[0] remains the same.

void p.insert(int i,Point_2 q) Inserts the vertex q before i.

void p.insert(int i,Point_2 list q) Inserts the list of vertex q before i.

void p.erase(int i) Erases the vertex pointed to by i.

void p.erase(int first, int last Erases the vertices in the range [first, last).

void p.push_back(Point_2 q) Has the same semantics as p.insert(p.size(), q).

void p.clear() Erases all vertices.

void p.poi_color(x,y,z) If color is called as p.fill() prints the color of the points Triangle_2
If it is called with with tuple (color.green) or (256,0,0) then it changes the color of the points of the Triangle_2.

void p.seg_color(x,y,z) If color is called as p.fill() prints the color of the segments Triangle_2
If it is called with with tuple (color.green) or (256,0,0) then it changes the color of the segments of the Triangle_2.

Predicates

bool pgn.is_simple() Returns whether p is a simple polygon.

bool pgn.is_convex() Returns whether p is convex.

bool pgn.is_empty() Returns pgn.size() == 0.

Orientation pgn.orientation() Returns the orientation of pgn.

Oriented side p.oriented_side(<Point_2> q) Returns POSITIVE_SIDE, or NEGATIVE_SIDE, or ON_ORIENTED_BOUNDARY, depending on where point q is. Precondition: p.is_simple().

Bounted side p.bounded_side(<Point_2> q) Returns the symbolic constant ON_BOUNDED_SIDE, ON_BOUNDARY or ON_UNBOUNDED_SIDE, depending on where point q is. Precondition: p.is_simple().

Point_2 p.left_vertex() Returns the leftmost vertex of the polygon p with the smallest y-coordinate.

Point_2 p.right_vertex() Returns the rightmost vertex of the polygon p with the largest y-coordinate.

Point_2 p.top_vertex() Returns topmost vertex of the polygon p with the largest x-coordinate.

Point_2 p.bottom_vertex() Returns the bottommost vertex of the polygon p with the smallest x-coordinate.

bool pgn.is_counterclockwise_oriented() bool pgn.is_clockwise_oriented () bool pgn.has_on_positive_side(<Point_2> p) bool pgn.has_on_negative_side(<Point_2> p) bool pgn.has_on_boundary(<Point_2> p) bool pgn.has_on_bounded_side(<Point_2> p) bool pgn.has_on_unbounded_side(<Point_2> p)

Polygon_2

Library Top

Releases

Show/Hide

Examples

Show/Hide

Classes

Point_2 Show/Hide

from eucleidis import * a = Point_2() b = Point_2(2,1) b.color(1,0,0) c = Point_2(1,2) c.color(color.red) c.color(color.green) d = Point_2(-1,2) c.color(visual.color.red) c.color(color.green) d.color(color.cyan) d.label("d")

Point_2 Library Top
Segment_2 Show/Hide

from eucleidis import * a = Point_2() b = Point_2(5,1) s1 = Segment_2(a,b) s1.color(1,0,0) c = Point_2(-1,2) d = Point_2(-1,5) s2 = Segment_2(c,d) s2.color(color.blue) s2.label("s2")

Segment_2 Library Top
Vector_2 Show/Hide

We are sorry but this class
(the vector or the direction) has no image.
This is because these classes
are only for intrenal purposes of the EucleiDIs library.
Try some other class in order to view pictures and code for this class.

Vector_2 Library Top
Direction_2 Show/Hide

We are sorry but this class
(the vector or the direction) has no image.
This is because these classes
are only for intrenal purposes of the EucleiDIs library.
Try some other class in order to view pictures and code for this class.

Direction_2 Library Top
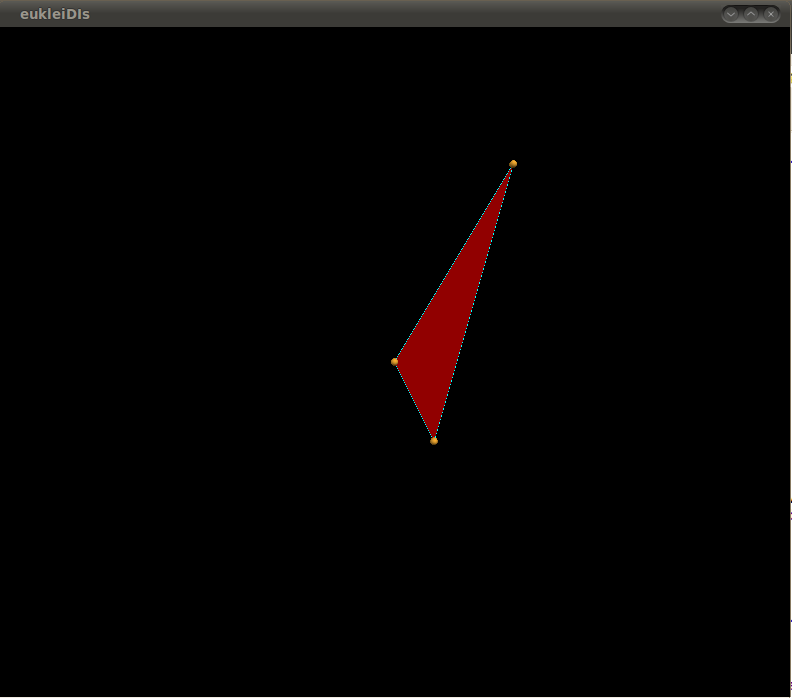
Triangle_2 Show/Hide

from eucleidis import * p1 = Point_2() p2 = Point_2(1,-2) p3 = Point_2(3,5) t1 = Triangle_2(p1,p2,p3) t1.area() 398.02512483510384 t1.orientation() 1 rorien[t1.orientation()] 'COUNTERCLOCKWISE' t1.seg_color(color.cyan) t1.poi_color(1,0.7,0.2) t1.fill(color.red)

Triangle_2 Library Top
Line_2 Show/Hide

from eucleidis import * p1 = Point_2() p2 = Point_2(3,4) l1 = Line_2(p1,p2) l1.color(0,1,0) p3 = Point_2(-1,5) l2 = l1.perpendicular(p3) l2.visual() True l2.color(1,1,0) l3 = Line_2(p3,p1)

Line_2 Library Top
Ray_2 Show/Hide

from eucleidis import * p1 = Point_2() p2 = Point_2(-1,-2) r1 = Ray_2(p1,p2) r1.color(0,1,1) r1.source().color(1,0,1) p3 = Point_2(6,2) r2 = Ray_2(p2,p3) r2.color(1,0,0) r3 = r2.opposite() r3.visual() True r3.color(color.orange)

Ray_2 Library Top
Circle_2 Show/Hide

from eucleidis import * p1 = Point_2() p2 = Point_2(4,5) c1 = Circle_2(p1,p2) c1.center().visual() True c1.center_color(1,0,0) c1.ring_color(0.5,0.7,0.2) c2 = Circle_2(c1.center(),p1) c2.ring_color(0,0,1)

Circle_2 Library Top
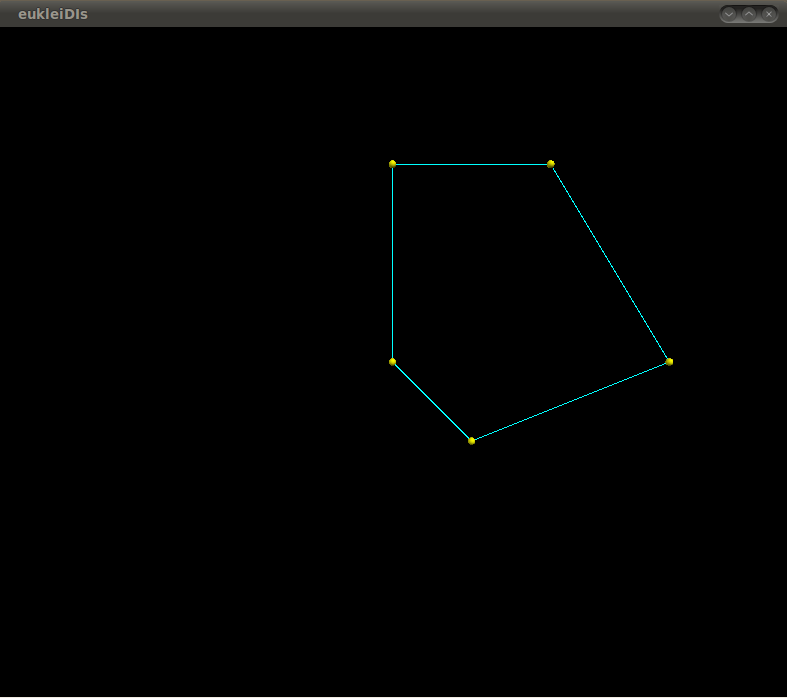
Polygon_2 Show/Hide

from eucleidis import * p1 =Point_2() p2 = Point_2(4,5) p3 = Point_2(0,5) p4 = Point_2(7,0) p5 = Point_2(2,-2) poly = Polygon_2([p1,p3,p2,p4,p5]) poly.poi_color(color.yellow) poly.seg_color(color.cyan)

Polygon_2