CHAOTIC COMMUNICATIONS AND SECURITY
Chaos-based security systems
CHAOTIC SIGNALS have been proposed as broadband information carriers with
the potential of providing a high level of robustness and privacy in data
transmission in the physical layer. Laboratory demonstrations of chaos-based
optical communications have already shown the potential of this technology,
but a field experiment using commercial optical networks has not been undertaken
until recently.For the very first time, the Optical Communications Laboratory
demonstrates high-speed long-distance communication based on chaos data
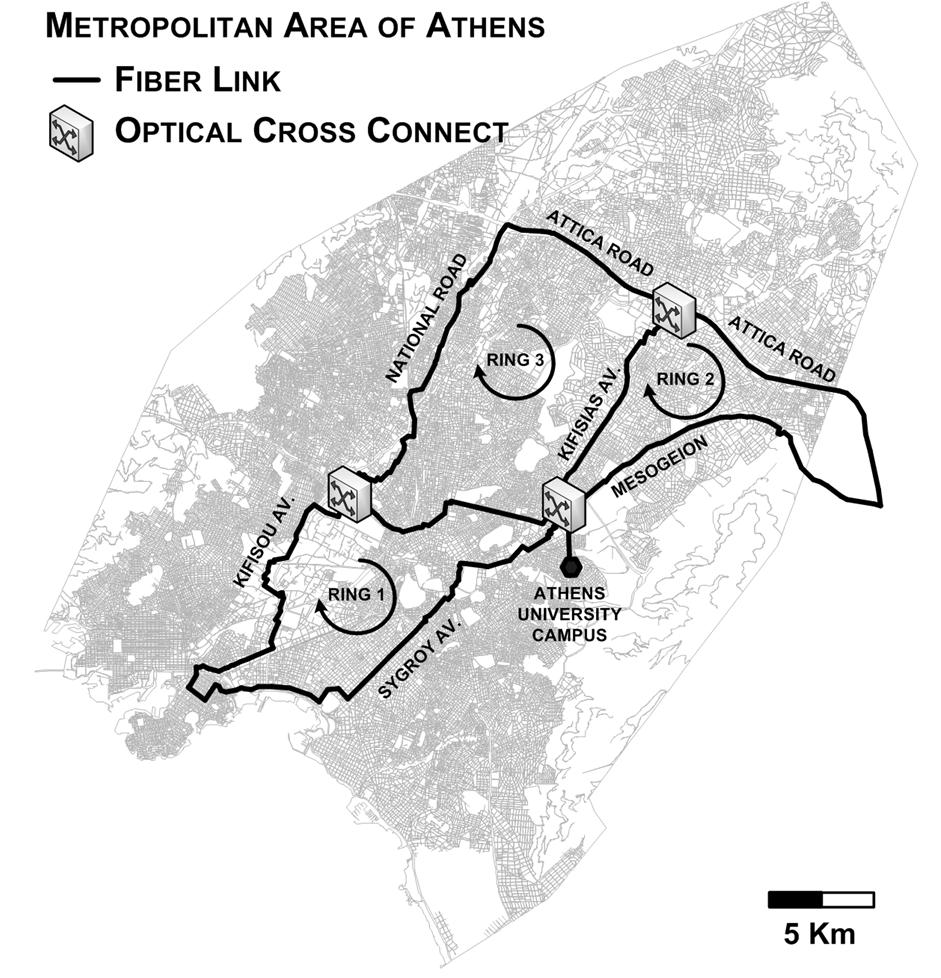
encryption over a commercial installed fiber-optic channel. A chaotic optical
carrier generated by a semiconductor laser is used to encode a message
for transmission over 120 km of optical fiber in the metropolitan area
network of Athens, Greece. The message is decoded using an appropriate
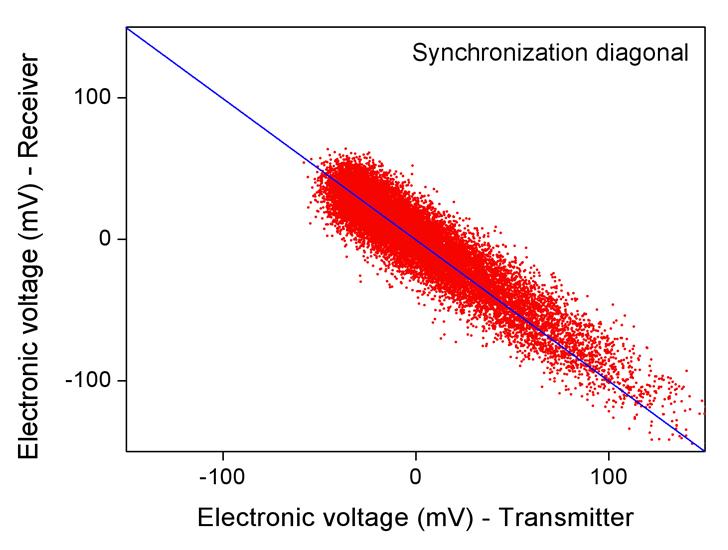
second laser which, by synchronizing with the chaotic carrier, allows for
the separation of the carrier and the message. Transmission rates in the
gigabit per second range are achieved, with corresponding bit-error rates
below 10 -7. The system uses matched pairs of semiconductor lasers as chaotic
emitters and receivers, and off-the-shelf fiber-optic telecommunication
components. Our results show that information can be transmitted at high
bit rates using deterministic chaos in a manner that is robust to perturbations
and channel disturbances unavoidable under real-world conditions.
The above results are presented, in collaboration with several first-class European Laboratories and Universities, in the 17 November 2005 issue of Nature Magazine (vol. 438, n. 7066, p. 343-346) entitled "Chaos-based communications at high bit rates using commercial fibre-optic links" by Apostolos Argyris, Dimitris Syvridis, Laurent Larger, Valerio Annovazzi-Lodi, Pere Colet, Ingo Fischer, Jordi Garcia-Ojalvo, Claudio R. Mirasso, Luis Pesquera and K. Alan Shore.
Most popular references:
Principle of operation
In the conventional communications systems an optical oscillator (semiconductor laser), generates a coherent optical carrier on which the information is encoded using one of the many available modulation schemes. On the contrary, in the proposed approach the transmitter consists of an optical oscillator forced to operate at the chaotic regime by an external feedback, producing thus an optical carrier with extremely broadened spectrum (in the order on many tens of GHz). The information (typically an OOK bit stream) is encoded on this chaotic carrier using different techniques (e.g. a simple yet efficient method is to use an external optical modulator electrically driven by the information bit stream while at its input is coupled the optical chaotic carrier). It is practically impossible to extract this encoded information using conventional techniques like linear filtering, frequency domain analysis or phase space reconstruction, assuming a high complexity in signal carrier and message amplitude that does not exceed a few percent of the amplitude of the chaotic carrier. At the receiver side of the system a second chaotic oscillator is used, as "similar" as possible to that of the transmitter. This "similarity" refers to:
The above set of hardware-related parameters constitutes the key of the encryption procedure.
THEORY ON CHAOTIC SIGNALS
One of the major characteristics and advantages of chaotic carriers is their unpredictability and extreme dependence on perturbations, parameters and initial conditions. There are many known algorithms and measures to quantify the complexity of such chaotic carriers and one of the tasks of our group is to measure them in detail as a function of the lasers' control and material parameters. A major activity of our group is to interconnect the complexity of the chaotic carriers (for applications to chaotic encryption) with the encryption efficiency using numerical computations of theoretical models.
We calculate numerically the Kolmogorov-Sinai entropy (metric entropy) hKS as a function of the control parameters that may easily change during an experiment (feedback strength and injection current) for open-loop and closed-loop configuration schemes. Also, the signal-to-noise ratio (SNR) is calculated in order to try to interconnect the chaos complexity with the encryption efficiency. The metric entropy is the most significant signature of strong or weak chaos since it measures the unpredictability of the chaotic carrier used for the masking of the transmitted message.
Hyperchaotic attractors (more the 1 positive Lyapunov exponents) are preferable for chaotic encryption applications since their reconstruction deteriorates for the eavesdropper, favoring therefore the security enhancement. Visualization of such chaotic attractors for the all-optical feedback case is given below where the carriers oscillate chaotically along with the electric field. Furthermore, bifurcation diagrams are plotted in order to investigate the dynamics properties in more detail such as routes to chaos and windows of periodicity.
The complexity of each chaotic carrier is evaluated -besides with the metric
entropy- with the Kaplan-Yorke (Lyapunov) dimension DL. High-dimensional
attractors (DL>>1) together with maximally chaotic attractors (hKS>0)
are ideal for applications to chaotic communications since they preclude
any adequate reconstruction attempt (with high Lyapunov dimension) and
also assure high unpredictability (with high metric entropy). Task of our
group is to seek the criteria for achieving such cases for the all-optical
feedback case. For the optoelectronic configuration, the dynamics fall
into the Ikeda-like scenario and complex chaotic dynamics are easier achieved
in contrast to the all-optical case since delay term (the delayed field)
is included in the nonlinearity.
Besides numerical calculations using approximate theoretical models (rate
equations), we focus as well on the complexity evaluation of experimental
data as a function of the control parameters. These calculations can be
inaccurate and notoriously difficult since they demand a large amount of
collected data points, closely spaced in time, and therefore we concentrate
on the range D2 < 6.5 where D2 is the correlation dimension. Significant
results have been deduced, from such data-analyses up to now that are found
to be consistent with theoretical and numerical predictions.
